George W. BUSH et le 11 septembre

Cette énergie de fracturation du béton est vraiment un sujet qui intrigue beaucoup les lecteurs. Hervé et Mathieu, entre autres, m'ont fait part de leurs questions ou de leurs doutes...

Certaines interrogations sont d'ailleurs très pertinentes et c’est vrai que la physique mise en jeu est encore mal maîtrisée car ce sont là des questions qui ont été très peu traitées dans le passé…

Ainsi, à force de muscapédication, les conspirationnistes poussent les scientifiques dans leurs derniers retranchements sur des sujets encore mal cernés… Cela explique pourquoi les derniers modèles, sortis 7 ans après la catastrophe commencent à peine à coller à peu près à la réalité. Je parle ici des modèles énergétiques car pour ce qui est de l’amorce de l’effondrement, après un minimum d'études sur la structure du bâtiment, les spécialistes ont su rapidement quelles avaient été les causes…

Mais avant d'entrer dans le détail d'explications plus techniques, je ferai dans un premier temps un simple appel au bon sens...

Si nous supposons que l’énergie développée par l’effondrement n'a pas été suffisante pour pulvériser le béton c’est que des explosifs ont été mis en œuvre. Imaginons donc 30 secondes le chantier...

Pour avoir de l’efficacité, l’explosif doit être mis au cœur du béton, et non contre, car les plaques en acier sur lesquelles il a été coulé l’auraient partiellement protégé… Cela veut dire qu’il faudrait faire tout un criblage par des perçages réguliers sur l'ensemble de la surface pour loger les charges, le tout sur 110 étages de 4000 m²… et ce dans les faux plafonds… sans que personne ne s’en aperçoive… avec les systèmes de mise à feu… des kilomètres de fils… et des centaines de détonateurs !!!

Mais au fait pourquoi faire ? Après avoir déjà prévu un avion et de la thermite (!) pour couper les colonnes et assurer la chute des tours, cela suffirait à créer l’émotion souhaitée, non ? Que les gens soient désintégrés dans l’effondrement ou écrabouillés entre deux dalles de béton c’est la même chose, non ?

C’est prendre des risques considérables, pour rien, que de mettre en place un tel réseau d'explosifs !

D'ailleurs, vu la taille du chantier, n'importe quel artificier vous dira que c'est quasiment impossible à réaliser : ils ne sont pas capables de gérer les microretards de déclenchement des explosions au-delà de quelques dizaines d'étage.

Dans la théorie du complot, l’idée qu’on ait pu faire « exploser » le béton est donc pour moi encore plus invraisemblable que la thermite. Il n’y avait vraiment aucun intérêt logique à une telle action sauf à risquer de se faire pincer en train de placer les explosifs ou de laisser des traces supplémentaires : charges non explosées, câblages de mise à feu résiduels, etc…

Sans parler des explosions : quand on connaît le bruit créé lors d’une DC pour saper une poignée d’éléments et ce après désossage complet du bâtiment (un chantier de plusieurs semaines), je n’ose même pas imaginer pour pulvériser 100 000 tonnes de béton !!!

Un calcul réalisé sur le site debunking911 montre que pour atteindre la même énergie que l’énergie potentielle d’une tour, il aurait fallu 212 tonnes de TNT… Donc si l’énergie gravitationnelle n’a pas pu pulvériser ce béton, combien en aurait-il fallu ?? 300, 400 tonnes ?? Ça en fait des semi-remorques... et une sacrée déflagration !

Le simple bon sens, et pas des kilomètres d'équations, amène donc à chercher une explication bien plus réaliste que l'explosif pour pulvériser le béton.

Maintenant, plaçons-nous sur un plan plus 'scientifique'...

L'énergie de fracturation, ce qu'elle caractérise

L'énergie de fracturation du béton est une notion qui a beaucoup de mal à passer chez les personnes ne connaissant pas bien le matériau.

Un premier élément qu'il faut absolument avoir en tête est que le comportement du béton est non symétrique : il résiste très bien en compression, mais très mal en traction.

Cela explique pourquoi vous pourrez casser aisément au marteau une plaque de 1 ou 2 cm d'épaisseur de béton mais pas un bloc de plusieurs centimètres. De la même façon, évaluer l'énergie nécessaire à la pulvérisation d'un béton avec une perceuse est parfaitement stupide car la perceuse travaille justement en compression c'est-à-dire de la pire façon qui soit pour rompre ce matériau. Pour fixer un ordre de grandeur, il est communément admis que le ratio entre la résistance en compression et en traction est de l'ordre de 10. C'est pour cela qu'on associe acier et béton pour créer du béton armé.

L’énergie de fracturation utilisée dans les calculs correspond précisément à l’énergie nécessaire pour fendre un béton par traction. Comme le béton résiste très mal en traction, cela donne une énergie très faible.

Il faut également noter que l’épaisseur dans le sens de l’effort de traction ne joue pas dans ce cas : imaginez deux cordes de 1 et 2 mètres de long. Si vous voulez les couper en deux par traction, c’est leur diamètre qui va compter, pas leur longueur. C'est pour cela qu'on évalue l'énergie par m².

Un autre élément remarquable en préambule, est qu'un solide soumis à de la compression (ou de la flexion) peut développer des contraintes de traction. C’est le principe qui est utilisé dans l’essai 'brésilien' pratiqué sur des éprouvettes de béton cylindriques. Nous le détaillerons dans le paragraphe juste en dessous.

La méthode utilisée pour déterminer cette énergie de fracturation repose un peu sur le même principe que l’essai mouton : des éprouvettes sont entaillées et on mesure l'énergie nécessaire à la propagation de la fissure.

La méthode est partiellement décrite dans la thèse de Fabien Delhomme, déjà donnée en référence. Je vous en propose un extrait ici.

Extrait de la thèse de Fabien DELHOMME (j'ai mis en gras les passages intéressants) :   Le béton, comme la pierre, et beaucoup d’autres matériaux, présente un mécanisme de fissuration différent de celui des métaux lors d’un mode de rupture par traction (mode I). Ils sont caractérisés par une zone de propagation de la fracture (« Fracture Process Zone : FPZ ») dans laquelle le matériau est soumis à de légers dommages [HIL, 76] [MOM, 03]. Dans l’acier, un matériau ductile, cette zone est quasiment inexistante car la zone endommagée passe directement d’un état élastique à un état plastique. En revanche, dans le cas du béton l’écoulement plastique est quasiment inexistant et la zone non linéaire est entièrement décrite par une FPZ : ce sont des matériaux quasi-fragiles [BOR, 96] [BOR, 02]. La figure IV.18 décrit un mécanisme de propagation d’une fissure dans un matériau tel que le béton.   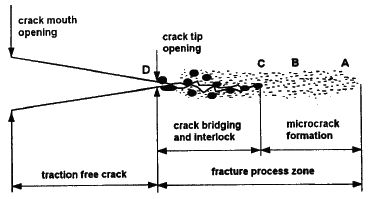« GF », correspondant à l’aire totale sous la courbe contrainte-ouverture de fissure (J.m-2), représente l’énergie totale dissipée par mètre carré de plan de fissuration lorsque les deux surfaces fissurées sont complètement séparées en un point donné.   Formule du comité Euro-International du Béton Formule proposée par Bazant     (Pour l'anecdote, l'un des rapporteurs de la thèse, Jacky Mazars, est un des plus éminents experts  français en matière d'étude de l'endommagement du béton)

Les deux formulations sont comparées dans la thèse, elles donnent des ordres de grandeur identiques. Ainsi l'énergie de fracturation est fonction de plusieurs paramètres : diamètre du plus gros granulat, résistance à la compression du béton, type de granulat et proportion de l'eau par rapport au ciment.

Concernant la valeur numérique choisie, notons tout d’abord que le béton utilisé sur les bacs en acier du WTC n’était pas d’une qualité exceptionnelle (1500 kg/m3 soit 35 % de moins qu’un béton normal). Sa résistance en compression, vu les connaissances à l’époque en matière de formulation et de fluidifiant chimique, ne devait donc être comprise qu’entre 15 et 20 MPa au maximum, contre 40 à 50 MPa pour les bétons « normaux ». En faisant l’application numérique pour fc28 = 15 MPa, d= 12 mm, granulat roulé, C/E = 0,7, cela nous donne la valeur de 45 Joules utilisée dans le calcul.

Par rapport à 100 J (béton normal), 45 J n’est donc pas irréaliste vu le béton considéré.

La taille des granulats ne joue-t-elle pas un rôle dans cette énergie ?

Cette question m'a été posée par Mathieu qui soupçonnait un comportement différent du matériau béton suivant si l'on s'intéresse à la pâte cimentaire ou au granulat (comportement hétérogène).

Pour mon explication, je prendrai l'exemple de l'essai de fendage brésilien (6.6.2 là) où une rupture verticale nette s'opère traduisant une mise en traction du béton. En effet, bien que le cylindre soit sollicitée en compression, il est facile de montrer que la direction perpendiculaire à l’axe de compression est soumise à une contrainte de traction. La démonstration fait appel à la mécanique des milieux continus et aux cercles de Mohr.

La rupture est alors régulière : non seulement la pâte cimentaire est fendue, mais aussi certains granulats qui sont cassés nettement (voir photo ci-dessous à droite).

Dans le cas de granulats roulés (extraits dans les cours d'eau et ressemblant à des galets) certains peuvent être décollés (voir la même photo) mais pour ceux qui sont concassés, c'est l'ensemble des grains situés dans le plan qui se rompent.

L'essai de fendage 'Brésilien'...

Cela montre que les résistances en traction de la matrice (les granulats) ou du liant (le ciment) sont de valeur équivalente. Dans la formule de Bazant ci-dessus, il est tenu compte du type de granulats qui peut améliorer l'adhérence liant/matrice.

Ce comportement voisin justifie qu’on ne tienne pas compte de l’effet d’échelle pour la fracturation de l’éprouvette de 8,7 cm.

A quoi peut-on comparer cette énergie ?

Hervé, qui est spécialiste de balistique, m'a proposé une comparaison avec les dégâts provoqués par des armes de guerre sur le béton. Les énergies des projectiles tirés par ces armes (Kalachnikov par exemple) sont de l'ordre de 2000 joules : les vitesses d'éjection peuvent atteindre mach 3 pour des balles de 7 à 8 grammes environ ! C'est vrai que cela peut laisser songeur par rapport à la valeur de 885 J/kg pour pulvériser le kilo de béton...

Mais il reconnaît lui même que cette comparaison n'est pas forcément pertinente en raison d'éclats, de projections et de forts échauffements. Il propose par contre une analogie plus intéressante entre l'effondrement des tours et un gigantesque concasseur... C'est aussi une comparaison que m'a proposée Mathieu avec deux liens d'articles à consulter : http://www.b-i-m.de/public/ibac/mueller.htmh et ttp://www.elorantaassoc.com/eob97.htm.

Dans le premier, on peut lire que l’’impact crusher’ (un concasseur) travaille à 1,5kWh/tonne soit 5400 J/kg de béton. Mais cette énergie est requise pour fracturer les bétons aux alentours de 2 mm, pas 100 µm.

Dans le deuxième, on apprend qu'une fracturation à 60 µm nécessite près de 22 kWh/tonne soit 79200 J/kg. En associant la formule proposée dans cet article et l’’impact crusher’, nous arrivons à 52000 J/kg pour des particules de 100 µm.

Ce qu'il faut bien comprendre, c'est que cette énergie est la puissance électrique consommée par les appareils de concassageet qu'elle est très supérieure à l'énergie réelle utilisée pour fragmenter le matériau, le rapport entre les deux définissant le rendement de l'appareil

En fait, l'énergie utile fournie au matériau pour son broyage mécanique est assez ridicule par rapport à la puissance de l'appareil et d'autant plus faible que le matériau est fin. Vous pourrez le lire sur cet article des Techniques de l'ingénieur. L'exemple d'un broyeur à boulets est donné, avec une énergie allant jusqu'à 36000 J/kg suivant le matériau pour des particiles de 100 µm, mais dont le rendement n'est que de... 2,7 % !

Si nous prenons 2,7 % de 36000 J, nous sommes à 970 J/kg mais il est très difficile et pour le moins aléatoire d'interpréter ces chiffres.

La taille des particules

Bien sûr, plus la taille des particules à générer est petite, plus l'énergie nécessaire est importante.

Il m'a été reproché de prendre 100 µm pour le calcul énergétique (grossier) que j'ai présenté, en me renvoyant sur une étude qui a été faite de la toxicité des résidus sur la zone du WTC. La médiane des tailles de particules pour ces échantillons se situe autour de 50 µm.

J'objecterai d ’abord, et c’est très simple à comprendre, que les lieux de prélèvement étaient loin des tours, tous situés entre 100 et 300 m. Il est donc normal qu’on ait trouvé à ces endroits-là les particules les plus volatiles, donc les plus fines. Les éléments plus lourds, pulvérisés plus grossièrement, sont au contraire restés au cœur de l’effondrement et au milieu des décombres. Pour l’instant je n’ai pas d’indication concernant une étude sur ces éléments là… Pourtant il y en avait.

Ensuite, dans ces particules, il n’y avait pas que du béton, mais aussi du plâtre (Gypsum) ou du flocage de protection incendie qui sont bien sûr beaucoup plus « tendres » que le béton…

La valeur de 100 µm prise comme valeur moyenne pour le béton n’est dons pas à mon sens irréaliste… D’aucuns la trouvent d’ailleurs bien trop pénalisante… Je reconnais que c’est un peu arbitraire mais on ne peut pas non plus prétendre que ce qui a été prélevé à 200 m du lieu de l’effondrement est représentatif des particules de béton dans leur ensemble… C’est scientifiquement absurde et surtout très loin de rendre compte de la réalité.

Lorsque j’écris l'hypothèse que TOUT le béton a été fracturé en particules de 100 µm, je suis donc extrêmement sévère dans mon choix.

Malgré cela, l'énergie potentielle est largement suffisante pour expliquer la pulvérisation du béton.

Ajout : quelques vues des décombres laissant apparaître un béton fracturé et non pulvérisé...

Beaucoup de correspondants me renvoient au site de Gage qui revendique maintenant près de 600 architectes et ingénieurs en faveur de la 'réouverture' de l'enquête.

Comme je l'ai écrit dans les news, précisons déjà que des articles dans des revues spécialisées et de renommée internationale continuent à paraître encore de nos jours sur le sujet, ce qui prouve bien que le dossier n'est pas clos.

Ensuite, je répète encore que parmi les 600 signataires seulement une poignée sont spécialisés dans le calcul de structures. Les autres sont des ingénieurs dans de tout autres domaines (électricité, statistiques, mécanique automobile ou aéronautique...) qui n'ont rien à voir avec le sujet traité !! Demanderiez-vous à votre boulanger de faire la révision de votre voiture ???

Un exemple accablant : Gordon Ross 'ingénieur en fabrication'... cet ingénieur a pondu un bon nombre d'articles, pour faire avancer la théorie du complot et surtout réfuter les arguments pro-VO avancés par des scientifiques de renommée internationale (Bazant, Greening...). Ses papiers sont en 'Une' du site de Gage. Le problème c'est que n'étant pas spécialisé en calcul de structures, il écrit des énormités. Par exemple dans cet article, il pose dès le départ des hypothèses tellement idiotes sur le comportement de l'acier vis à vis du flambement que l'ensemble est à jeter : comme nous l'avons vu, le flambement n'a jamais été dépendant de la déformation (epsilon) du matériau mais des caractéristiques de ce matériau et de la géométrie de l'élément... J'écris 'idiotes' pour rester poli et courtois car ce n'est même pas digne d'un étudiant d'IUT génie civil. Que d'énergie perdue à écrire ce genre d'inepties ! Crédibilité de cet ingénieur pour parler de génie civil ? Zéro ! Zéro de chez zéro.

N'oublions pas que ce n'est pas parce qu'une poignée de spécialistes (je dis bien une poignée) avance une thèse que c'est une vérité. Sinon, cela voudrait dire qu'il n'y a jamais eu de chambre à gaz pendant la seconde guerre mondiale, ou que l'eau a une mémoire d'éléphant...

Il m'est souvent reproché par mail de ne pas tenir compte du contexte géopolitique dans mes analyses...

Au risque de me répéter, je précise bien que ce site n'a pas pour but de démontrer que la théorie du complot est exacte ou farfelue... L'objectif est de dénoncer tous les arguments scientifiques fantaisistes qui sont utilisés pour étayer cette thèse pour tout ce qui concerne l'effondrement des tours ou le crash sur le pentagone.

Ce qui s'est passé avant (qui était dans les avions et pourquoi ?) ou après les attentats (invasion de l'Afghanistan ou de l'Irak) nécessite des investigations et des connaissances en géopolitique qui me dépassent largement... Je ne vais pas faire ici ce que je reproche à d'autres personnes qui s'improvisent spécialistes en mécanique des structures ! Je laisse donc ça à d'autres, beaucoup plus compétents que moi. Certes j'ai bien quelques idées, mais elles tiennent plus de la 'brève de comptoir' que d'une analyse experte et circonstanciée. Par exemple, je n'ai jamais cru aux armes de destruction massive en Irak (comme la majorité des français d'ailleurs) et je pense Ben Laden mort et enterré... Mais ce n'est que mon avis.

Tout cela n'a eu et n'aura jamais aucune influence sur la Physique et la Mécanique : pas besoin de considérations géopolitiques pour étudier la résistance des matériaux dans les tours du WTC ou dans le Pentagone !

Je vais répondre ici aux commentaires et critiques formulés par F. Henry-Couannier sur son site...

En préambule, je souhaite souligner que je ferai abstraction des propos grossiers et scatologiques dont il est coutumier. Les plus curieux pourront aller lire sur son site et le forum de zététique quelques exemples gratinés. Je ne mettrai pas non plus en avant sa suffisance et son ton péremptoire, chacun pourra juger…

De cette longue diatribe (plus de 40 pages une fois imprimée) que retenir ? Je ferai ressortir trois points importants.

1) Rien de nouveau sous le soleil de Marseille

Tout au long de cette page interminable, le lecteur n’a droit à aucun élément nouveau, seulement des affirmations qui ne s’appuient sur aucune preuve vérifiable.

La seule chose qui intéresse F. H.-C. c’est la thermate et les thermobariques… On sent bien que ça devient obsessionnel ! Malheureusement ce n’est pas en sautant nerveusement à pieds joints et en criant 'thermate' et 'thermobarique' à qui veut l’entendre qu'il convaincra les scientifiques dignes de ce nom...

Pour la thermate, par exemple, il s’appuie sur les résultats de la Fema et Jones qui ont trouvé des traces de sulfuration sur l’acier du WTC… Le problème, c’est qu’au lieu de chercher comment l’énorme quantité de plâtre en suspension dans l’air et dans les décombres aurait pu interagir avec de l'acier à haute température (et pas nécessairement en fusion), on conclut tout de go quec’est de la thermate et pas autre chose !…

Affirmations gratuites, conclusions à l’emporte pièce…

Jones nous avait habitué à cela : d’abord sur la fusion froide, ensuite sur la visite de Jésus après sa résurrection chez les Mayas (une charmante excursion à n'en pas douter), 'démontrée', défense de rire, à partir de l’analyse de... gravures autochtones ! Cela n'étonnera donc personne qu'il trouve de la thermate sur les colonnes du WTC...

Ce qui est plus inquiétant, c'est que F. H.-C. lui emboite le pas... et à grand pas !

En plus, comme si cela ne suffisait pas…

2) Il persiste dans l’erreur et ne se remet jamais en question

Les erreurs ? il rame fort pour le minimiser (en rouge ce qui est écrit sur son site)...

+ Tour Windsor de Madrid ? la comparaison joue un rôle mineur, pourtant Gage continue à l’utiliser, notamment dernièrement à Genève !!! F. H.-C. l’a sortie par contre de son diaporama… c'est tout à son honneur.
+ La photo bidonnée ? Gage n'en aurait eu connaissance qu'après coup, peut être, mais alors pourquoi ne pas l’avoir dénoncée ? Surtout que vu le style de prise de vue (souvent face à la caméra) cela tient plus du film de propagande que de l’interview. J’ai donc du mal à croire qu’il n’a pas participé au montage !! 
+ Les vidéos tronquées ? il justifie cela par une interview limitée dans le temps… ben voyons, alors que les commentaires sont en arrière-plan, ce n’est pas les deux secondes de l’effondrement initial qui font changer la face de l’interview !
+ La pression négative ? Gage veut évidemment parler d'une dépression... Merci, j’avais compris !! c’était juste pour montrer le degré d’approximation scientifique de ses interventions…
+ pas de force d’effondrement ? en gros, Gage a raison car pas d'accumulation de débris au centre (pied des tours!!) justification incroyable alors qu’il y avait l'équivalent de plusieurs étages de débris amoncelés si on compte les sous- sols (voir la photo, là, vers la milieu de la page) !!
+ la faible épaisseur des dalles de béton et leur densité pour expliquer la pulvérisation : Détails insignifiants… !!!

Plus grave...

* quand un fait le dérange, F. H.-C. met en doute ou dénigre les travaux de scientifiques qui ont bossé parfois pendant toute une vie sur le sujet : la fracture de la pâte cimentaire et des graviers par exemple…
Des articles sont sortis sur le sujet et n’ont rien à voir avec le 11 septembre… Bien sûr, cela dépend des granulats, mais on arrive à avoir pour certains bétons des résistances de la pâte cimentaire supérieures à celle des graviers. (j’ai les articles sous le coude pour ceux qui souhaitent). En particulier dans le cas du WTC où on a souhaité utiliser des bétons extrêmement légers, il ne serait pas étonnant que les granulats aient eu des résistances bien moindres que les granulats classiques, et donc que le mortier.
* F. H.-C. jette aussi son fiel sur les revues et articles à comité de lecture… C’est justement pour éviter des articles sans aucun fondement comme on peut le voir sur le site de Gage que ce système est utilisé !

3) Malgré tout quelques points où l’on se rejoint…

Le Pentagone… Il n’y a plus que les gens de mauvaise foi pour croire encore au missile ou a une bombe...

F. H-C. utilise sans vergogne les interprétations que j'ai faites sur les 'squibs' pour les arranger à sa sauce...

Et même pas un merci avec ça !! )

[Au passage petit debunking (désolé je ne peux pas m'en empêcher...) Effectivement, les surpressions ont été communiquées en aval du front de l'effondrement par les circulations horizontales et verticales. Mais ce n'est bien évidemment pas des pseudo-bariques explosives qui ont créé ces surpressions. Hydrogène ou fioul, peu importe.... on aurait entendu les explosions plusieurs kilomètres à la ronde.

D'ailleurs comment expliquer que les thermobariques remplies de fioul (100, 200... 500 litres par étage ??) feraient plus de dégâts que 30 000 litres de kérosène sur une zone extrêmement réduite de 2 à 3 étages ? Je n'ai pas vu de béton pulvérisé lors du crash des avions... Bizarre, non ? C'est bien la preuve que si la charge explosive n'est pas logée au cœur du béton (par des perçages à réaliser sur toute la surface) elle n'aura qu'un effet très réduit pour sa "pulvérisation"... C'est le B-A-BA du métier d'artificier.

Le plus savoureux, c'est que cette interprétation n'a été introduite qu'après une mise à jour : au départ, le commentaire était le suivant : N'importe quoi ! si une surpression brusque est à l'origine des squibbs il faudrait donc admettre qu'elle etait suffisamment puissante pour ejecter du béton pulvérisé à 200 km/h mais suffisamment peu puissante pour ne le faire que par la fenêtre la plus fragile alors que evidemment une telle impulsion de surpression devait s'appliquer également à toutes les fenêtres d'un étage donné (il n'y avait pas de cloisons au WTC mais un immense espace de bureaux entre les colonnes internes et exterieures). ... Ces arguments sont d'un niveau consternant... mieux vaut en rire !

Tellement consternant que maintenant il les reprend à son compte !! Sans commentaire...]

Pour les courageux, plus de détails là.

Un internaute qui intervient sur différents forums m'a invité à la relecture de cet 'article' tout récent (janvier 2009) :

http://journalof911studies.com/volume/2008/TheMissingJolt4.pdf

Comme il m'a proposé cela un samedi soir et que je pensais passer enfin un WE tranquille, sans bastison, je lui ai dit que ma réponse interviendrait sous quelques semaines, comme c'est de rigueur pour la revue d'articles scientifiques...

En fait, pris par le jeu et la curiosité, je m'y suis plongé dès le dimanche matin et force est de constater que la lecture s'est vite interrompue compte tenu du niveau de ce qui y est écrit...

Les deux auteurs prétendent réfuter la théorie de Bazant et du Nist en étudiant la vidéo de l'effondrement de la tour Nord. Pour cela, ils analysent image par image, comptent le nombre de pixels, pour finalement obtenir le déplacement du toit de la tour en fonction du temps.

Leur conclusion est que le bloc supérieur subit une accélération constante ce qui est bien sûr en contradiction avec l'hypothèse des chocs successifs des différents planchers.

Cela peut être visualisé sur le graphe qui suit, où ils obtiennent une courbe quasiment linéaire de la vitesse en fonction du temps.

Attention : cette courbe est issue d'une première version de l'article

(nous verrons plus bas la nouvelle version)

Le problème est qu'avec les données qu'ils fournissent, cette courbe est fausse ou tout du moins très imprécise !

En effet, pour calculer cette vitesse, ils moyennent l'accélération pour chaque pas de temps depuis l'instant t0 (p8 : a=2d/t²), puis recalculent la vitesse par v=v0+at.

Or, il est bien évident que cette accélération n'est pas constante depuis l'instant t0, en particulier en raison des chocs entre les planchers qui se produisent. Il est donc stupide d'en faire une moyenne pour estimer ses variations !

Même s'il est difficile d'interpréter les résultats avant t=1s compte tenu de l'imprécision des mesures, il est possible de tracer la courbe des vitesses pour chaque pas de temps par la formule vi=(di - di-1)/(ti - ti-1) (moyenne sur le dernier intervalle de temps) ou encore vi=(di+1 - di-1)/(ti+1 - ti-1) (moyenne sur deux intervalles de temps autour du point considéré)...

On obtient alors les courbes suivantes :

Vous conviendrez que ce ne sont pas exactement celles de Mac Queen et Szamboti !!!

La courbe jaune (deuxième formule) a bien entendu tendance à « lisser » les vitesses. Sur la rose (première formule), on peut supposer (je dis bien supposer) que les sauts correspondent à des impacts. Pas sur les premiers points puisque la mesure n’est pas suffisamment significative, mais à partir de 1,5 seconde, pourquoi pas ? (ratio [précision mesure/intervalle mesuré] < 0.33 pour la rose, < 0.16 pour la jaune à partir de 1.34s). De toute façon MacQueen et Szamboti ne s'embêtent pas, eux, avec ce genre de considérations : les chiffres et courbes sont donnés 'bruts de fonderie' comme autant de vérités indiscutables !

Remarquons au passage que les sauts ont tendance à s'estomper au fur et à mesure de l'écoulement du temps, ce qui peut traduire le fait que l’inertie du plancher impacté devient faible par rapport au reste des éléments au-dessus.

Tout cela me fait dire que l'article est complètement à côté de la plaque car ensuite, les auteurs se servent du fait que leur courbe est 'lisse' pour 'démontrer' que les impacts entre planchers n'ont pas décéléré la chute du bloc supérieur !

Autrement dit, après un lissage de courbe qu'ils imposent, totalement absurde sur le plan scientifique, ils s'écrient : vous voyez bien qu'il n'y a pas de saut dans le graphe des vitesses !!!

Une analyse un peu plus détaillée là.

Et un bonus...

Après Ross, voici donc MacQueen et Szamboti comme nouveaux théoriciens de la mécanique élémentaire...

Décidément, le site "journalof911studies" est bien parti pour être élu pire site scientifique de la toile !

En tout cas, le fait que de tels articles puissent être publiés en dit long sur la qualité du comité éditorial de ce site...

Remarque : l'article des deux 'scientifiques' susmentionnés évolue chaque jour sur le site de Jones pour récupérer ce qui est encore récupérable, c'est à dire... rien. J'ai eu la bonne idée de garder en archive la première version de l'article : ça va devenir un collector !...

La nouvelle version présente cette courbe :

Vous noterez que McQueen et Szamboti prennent deux intervalles de temps pour lisser autant que faire se peut les points (courbe jaune au-dessus) et se gardent bien de tracer la courbe correspondante...

Après trois mois passés à construire et alimenter bastison.net, un premier bilan et quelques perspectives…

PREMIER BILAN

D’abord, j’attire l’attention du lecteur sur le fait que je me suis toujours attaqué aux leaders du mouvement et jamais à ses sympathisants car je comprends très bien que des non-initiés puissent être trompés par les méthodes très pointues employées : savants enrobages, raccourcis foireux, bourrage de crâne, etc...

Malgré tout, il est frappant de voir dans cette affaire comment une poignée d’individus (Gage, Jones, Griffin...) a réussi à entourlouper autant de monde.

Car rappelons ici que ce mouvement ne repose sur rien de scientifique : ces gens ont basé toute leur démonstration sur le fait que les tours (1,2 ou 7) ne pouvaient s’écrouler du seul fait du crash des avions et/ou du feu, ce qui est dès le départ une escroquerie scientifique et intellectuelle monumentale.

Comme expliqué dans les différentes pages du site, la stabilité structurelle n’est assurée que pour une paire d’heure maximum (en France tout du moins) et à partir du moment où les moyens anti-incendie étaient inopérants (pompiers ou sprinklers) il n’y avait aucune de raison que ces bâtiments restent stables plus longtemps en raison de leur structure en acier. Et encore moins pour les tours 1 et 2 dont les protections passives ont dû voler en éclat lors de l’explosion du kérosène...

Disons le clairement : autant je peux comprendre que la façon dont c’est présenté trompe des personnes non averties, autant je trouve malhonnête de propager de telles bêtises de la part de ceux qui ont (en théorie) les capacités et les moyens de se renseigner auprès de personnes compétentes.

Après maintes lectures des articles parus sur le catastrophique 'journalof911studies' je le dis sans ambages : ce site est un monument de désinformation. 
On y trouve tout un tas de pseudo spécialistes qui viennent disserter sur la mécanique des structures et qui n’ont réussi qu'à produire un tissu d’inepties. La plupart sont atteints d'une forme très sévère de flatulence supra rectale et tentent de nous faire croire que des physiciens (Jones), théologiens (Mc Queen, Griffin), ingénieurs de mécanique (Szamboti, Ross), ou architectes(Gage) peuvent devenir spécialistes de calcul de structures en regardant quelques vidéos sur le net. 
Nous sommes face à du grand Guignol comme en attestent de façon flagrante les 'articles' pitoyables qu’ils ont pondus… Peut-être sont-ils compétents dans leur domaine, je n’aurai pas personnellement l’outrecuidance de les juger sur leur matière de prédilection puisque je n’y connais rien, mais pour la mécanique des structures ils peuvent repasser !… Passons donc…

Si je me suis attaqué aux 'icones' du mouvement, j’ai aussi tenté de dialoguer sur le forum de ReOpen… Hélas au bout de trois posts, les hors sujet, les procès en incompétence, voire les insultes, fusent… Le dialogue calme et serein ne semble pas de mise sur ce forum. 
Certains sont ouverts, le dialogue intéressant, mais d’autres sont assez obtus et par leur posts débiles arrivent à faire tourner court la discussion. La plupart de ces tristes sires ont d’ailleurs déversé leur fiel dans les commentaires du dossier consacré au sujet sur le site Rue89. Pas très glorieux…

Je veux bien d’ailleurs reconnaître que les articles de Rue89 sur le 11/09 peuvent manquer de précision. Par exemple, j’ai dû signaler que les colonnes centrales du pentagone étaient bien en béton armé et non en acier. La correction n’a pas encore été faite à ce jour… Sur un autre article (fonte de l'acier dans les décombres), les journalistes ont pris une hypothèse formulée surbastison.net et l’ont assénée comme une vérité sans me consulter... C’est bien sûr discutable ! Mais même avec ces imprécisions, le dossier est très complet et offre une base de discussion.
Par contre, la réponse qui a été faite par ReOpen sur son site procède des mêmes méthodes que Gage et consort : on sort une phrase du contexte et on lui fait dire le contraire de ce qu'elle prétend... Par exemple sur la chute libre concernant les tours 1 et 2 où j'ai écrit que les tours 1 et 2 (et non la 7) n'étaient jamais tombées à la vitesse de la chute libre... et bien sûr je le maintiens. On s'en sert pour dire que je n'ai pas lu le rapport Nist de la tour 7 alors que justement j'explique sur le site pourquoi on a pu observer une accélération proche de la chute libre sur cette tour !... Idem sur la fonte de l'acier où on ne prend même pas le temps de lire ce qui est écrit en détail sur le site. Le procédé est mensonger et malhonnête mais au fond ne m'étonne pas...

PERSPECTIVES

De nombreux internautes m’on contacté suite à cet article pour me remercier et m’encourager à poursuivre le travail… Merci à eux.

Le site en lui-même devrait peu évoluer. Tous les thèmes techniques ont été abordés, sans aucun tabou. Je n’irai surtout pas sur d’autres terrains (je n’en ai pas les compétences) pour ne pas prêter le flanc à la critique. Pour l’instant, les attaques ont d’ailleurs plutôt porté sur la forme que sur le fond et c'est bien compréhensible : tout ce qui est affirmé est connu depuis 40 ans ou plus sur le plan scientifique et les points douteux ou les hypothèses sont bien sûr traités au conditionnel.

Malheureusement, beaucoup ne font pas la différence entre les deux approches. C'est vrai que cela demande une lecture plus approfondie... Par contre, avec les tristes sieurs Jones, Gage et consorts, pas besoin de se poser la question : eux sont surs de leur fait, n'ont aucun doute ! Cela dénote entre une fois leur piètre rigueur scientifique...

Concernant ReOpen, je me demande si un jour ses adhérents seront satisfaits, leur devise est :

« Posons des questions, exigeons des réponses ».

Certes des questions peuvent et méritent d'être posées, encore faudrait-il accepter les réponses !

Et ce, même si elles ne vont pas dans le sens que l'on souhaite. Car pour arriver aux conclusions de Jones, Gage, Ross et Szamboti, il va falloir tordre la physique en 4 !!!

Je me propose même, si les personnes ouvertes au dialogue avec qui j’ai pu discuter sur Reopen veulent venir échanger dans mon labo, de les recevoir. Nous pourrions aborder 10 000 autres aspects de la mécanique des structures que je n’ai pas eu le temps d’exposer sur mon site, mais bien entendu, cela ne pourra se faire que dans le cadre d’un dialogue courtois et ouvert... 

(posté également sur le forum de ReOpen)

Ou plutôt le non basculement !... (rédigé suite à la question de Marco)

Nous avions vu précédemment qu'un côté de la tour WTC2 avait été fortement affaibli et qu'elle avait eu tendance à basculer d'un côté dans les premières secondes, pour ensuite suivre un processus identique à celui de la tour 1.

Une question que se pose souvent un observateur lambda est donc : pourquoi la tour n'a-t-elle pas complètement basculé ?

Une première ébauche a été fournie par Bazant et Zhou dans leur article datant de 2002 pour expliquer cela.

Mais pour comprendre ce phénomène, il est aussi possible de faire une analogie avec de la démolition contrôlée car la première partie de l'effondrement ressemble, géométriquement, à ce qui est appelé par les experts un "basculement à charnière haute".

Ce qui nous est justement dit dans cet article des 'Techniques de l'Ingénieur', c'est que lors de tout basculement provoqué par charnière, il se crée au niveau du pivot (l'endroit où la rotation se produit) une composante horizontale liée au mouvement de l'ensemble. Cette action peut atteindre 20% du poids total supporté ce qui peut nuire au basculement de la tour si les ingénieurs n'en tiennent pas compte. En effet, dans le cas où cette charnière vient à lâcher avant que le bloc n'ait totalement basculé, on en revient exactement à une technique d'effondrement par 'simple' foudroyage... et la chute du bloc se fait donc verticalement. Or, la composante statique horizontale la plus forte pour laquelle les tours avaient été dimensionnées était bien sûr le vent. Cela peut expliquer pourquoi les boulons qui assuraient la liaison entre les colonnes de façade ne permettaient de reprendre au mieux, après un rapide calcul, que la moitié de la rotule plastique admissible par les poutres.

Comme les colonnes n'avaient pas été conçues pour supporter cette énorme composante horizontale, il est évident que les liaisons se sont rompues bien avant que le centre de gravité du bloc supérieur sorte de la ceinture périphérique constituée par les colonnes de façade. Il aurait fallu atteindre un angle d'environ 35° pour que ce centre de gravité sorte de la base de la tour.

Là, ce ne fût pas le cas, résultat : le basculement total n'a pu se produire et la descente du bloc s'est alors poursuivie verticalement.

D'ailleurs, le fait que la rotation se soit interrompue montre bien qu'il y a eu une résistance à cette rotation et qu'elle a compensé l'inertie acquise précédemment... Cela prouve que les étages inférieurs ont réellement résisté et n'ont pas été "anéantis" par des explosifs ou tout autre artifice : la résistance était suffisante pour freiner le basculement mais insuffisante pour arrêter l'effondrement global.

Il est possible de voir clairement l'arrêt de la rotation sur la fin de cette vidéo...

Le texte de l'article lié au basculement par charnière haute...

Pourquoi les tours 1et 2 se sont-elles effondrées de façon parfaitement verticale, en suivant leur axe ?...
 

Cette interprétation est justifiable par les observations qui ont été faites. Sur une vidéo présentée par ailleurs, nous avions déjà vu que lors de l'effondrement de la tour Nord (la deuxième à s'effondrer), une partie du cœur est restée en place pendant quelques secondes.

Des photos qui sont moins connues, mais encore plus intéressantes, sont celles de Aman Zafar et concernent la tour sud. Elles montrent clairement qu'une grosse partie du noyau est restée bien présente au cours de l'effondrement. Vous trouverez les originales là.

Aman Zafar indique sur son site que les deux dernières photos ont été prises avec un intervalle d'environ 10 secondes. Ce délai semble exagéré compte tenu des vidéos disponibles, mais sur l'avant dernière on distingue nettement le noyau de la tour et sur la dernière on devine la partie haute qui finit de s'enfoncer dans le nuage de poussière.

Il est vraiment dommage qu'aucune vidéo ne montre l'effondrement de la tour sud depuis cet angle, cela aurait permis de voir précisément comment le noyau est resté érigé. Quoiqu'il en soit, sans plus aucun élément de stabilisation (les planchers) il ne pouvait plus tenir, même sous l'action de son seul poids propre. L'élancement devenant trop important les colonnes ne pouvaient que céder.

Or, il n'y a pas cinquante solutions : si des explosifs ont été utilisés AVANT l'effondrement, pourquoi le cœur ne s'est-il pas effondré en même temps que le reste ? Quant à espérer que ces explosifs aient agi APRES l'effondrement des planchers, vu le capharnaüm, c'est bien sûr totalement illusoire.

De nombreux témoignages ont fait état d'explosions survenues dans les tours, parfois avant, pendant ou après le crash des avions.

L'un des plus célèbres de ces témoins est William Rodriguez, il a sauvé plusieurs personnes à l'intérieur de la tour ce jour là. Il travaillait dans un des sous-sols et a secouru des gens qui avaient été brulés par la boule de feu qui s'était engouffrée dans les circulations verticales : escaliers et ascenseurs. Un site a été créé tout à sa gloire...

Malheureusement, en y regardant de plus près, on s'aperçoit que le témoignage de cette personne est tout sauf fiable. Mark Roberts, qui est aux Etats-Unis LE pourfendeur des thèses conspirationnistes, a créé une page spécialement dédié aux assertions de William Rodriguez. Ses revirements, contre-vérités pour ne pas dire mensonges y sont méticuleusement recensés...

http://911stories.googlepages.com/home

Il est possible de lire également (en bas de page) tout un tas de récits qui montrent que du sous-sol jusqu'à l'étage directement sous le crash des avions, il est possible d'avoir tous les témoignages que l'on souhaite, aussi contradictoires les uns que les autres : certains n'ont même pas entendu l'avion et ont cru à un tremblement de terre alors qu'ils étaient une poignée d'étages en dessous de l'impact... Cela corrobore parfaitement la thèse des hologrammes : il n'y a donc pas eu d'avion sur les tours !...

Je plaisante bien entendu, mais cela montre bien qu'avec cette multitude de récits n'importe qui peut arriver à n'importe quelle conclusion.

Mark Roberts intervient souvent sous le pseuso Gravy sur le forum de la James Randi Educational Foundation (JREF). Une zone estréservée aux thèses conspirationnistes, tout y est abordé et démonté point par point. C'est une mine d'informations. Depuis plusieurs années Gravy répond sans relâche aux questions et dénonce les approximations... Son abnégation et sa patiente sont remarquables !!

William Rodriguez, ou Bjorkman ('la recrue du mois' pour février 2009 sur le site de Gage !) ont également posté sur ce forum pour essayer tant bien que mal de défendre leurs positions...

Les explosions avancées par Rodriguez et d'autres ont été expliquées maintes fois, vous trouverez tout cela aisément sur la page de Mark Roberts, mais en gros, il y a eu la boule de feu due au kérosène, les chutes d'ascenseurs, les conséquences des incendies.

Ross (encore lui !!) a essayé de montrer que des déflagrations avaient été enregistrées sur les relevés sismiques du 11/09.

Malheureusement c'était tout aussi foireux que ses tentatives de calcul de mécanique des structures... Force est de constater que son article (coécrit avec Furlong qui est intervenu lui aussi sur le forum JREF pour défendre l'indéfendable) est encore accessible sur le site de Jones... Cela démontre encore une fois la malhonnêteté et l'incompétence crasse de ce site !!

Ajoutons qu'il est connu qu'en situation de grand stress (ou non d'ailleurs), les témoignages humains sont ce qu'il y a de moins fiable sur le plan scientifique ! Je vous propose à ce propos quelques lectures édifiantes :

Les ovnis et les illusions du cerveau

Peut-on faire confiance à un témoignage ?

Elizabeth Loftus, une référence en matière d'étude de fiabilité des témoignages

Comment se construire de fausses croyances ?

Epistémologie du témoignage : la dépendance épistémique de la parole des autres
La fragilité du témoignage

Les enlèvement d'humains par les extraterrestres : une triste réalité !

La vérité sur les enlèvements extraterrestres

L’irruption de mondes intermédiaires ? Le cas des Ovnis

C'est pourquoi prendre quelques témoignages allant dans un sens, tout en écartant tous ceux qui vont les contredire de manière flagrante, procède d'une grande malhonnêteté intellectuelle.

Edition du 14/07/2009...

Sans parler des témoignages qui se révèlent de manière, comment dire ?... tardive !! Trouvé sur le forum des sceptiques du québec, un post de Lambert85 intégralement reproduit ici... Passionnant.

Que rajouter à cela ?

Edition du 06/09/2009...

Cela montre encore une fois le peu de fiabilité des témoignages dans des situations aussi confuses : les notions d'espace et de temps sont altérées et les témoignages sont complètement faussés.

Et pour conclure cette rubrique, quelques bruits sourds "d'explosions" liés à la ruine d'une structure métallique.
Des sons qui se produisent AVANT l'effondrement, le bâtiment étant en construction, non clos, et même pas en feu !...

Trois victimes dans cet accident.

Retour en haut de la page

Page d'Accueil

Souvent on me demande d'où vient le nom de bastison.net...

Bastison est un terme occitan qui signifie maison, construction. La prononciation exacte est "bastizou".

Au moment de choisir un nom pour ce site, le terme 'construction' était bien sûr utilisé avec toutes les extensions possibles puisque la même ortographe est utilisée dans plusieurs langues.

J'ai donc pensé que prendre un nom occitan serait un joli pied de nez face à l'uniformisation (pour ne pas dire l'américanisation) des cultures...

Donc sur ce plan là aussi, bastison.net peut être considéré comme une forme de résistance face aux travers du net !!!